Question

Trigonometry . What

Answer 1

Ques 11: 123.08 meters.

Ques 12: 269.4 meters.

Ques 13: 211.27 meters.

Explanation:

Ques 11: We have that the angle of elevation from the ship to the top of the lighthouse is 18° and the height of the lighthouse is 40 m.

It is required to find the distance of the ship from the shore, say 'x' m.

As, we have,
`\tan \theta=(opposite)/(adjacent)`

⇒
`\tan 18=(40)/(x)`

⇒
`x=(40)/(\tan 18)`

⇒
`x=(40)/(0.325)`

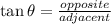
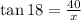
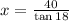
⇒ x = 123.08 m.

Thus, the distance of the ship from the shore is 123.08 meters.

Ques 12: We have, length of the kite is 300 m and the angle made by the string is 64°.

It is required to find the height of the kite, say 'x' m.

As, we have,
`\sin\theta=(opposite)/(hypotenuse)`

⇒
`\sin 64=(x)/(300)`

⇒
`x=300* \sin 64`

⇒
`x=300* 0.898`

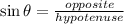
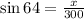
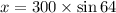
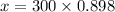
⇒ x = 269.4 m.

Hence, the height of the kite is 269.4 meters.

Ques 13: We have, the wreckage is found at the angle of 12° and the diver is lowered down by 45 meters.

It is required to find the distance covered by the diver to reach the wreckage, say 'x' m.

As, we have,
`\tan \theta=(opposite)/(adjacent)`

⇒
`\tan 12=(45)/(x)`

⇒
`x=(45)/(\tan 12)`

⇒
`x=(45)/(0.213)`

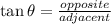
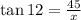
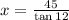
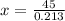
⇒ x = 211.27 m.

Thus, the distance covered by the diver to reach the wreckage is 211.27 meters.