Answer:
Price of an adult ticket is $3 and price of student ticket is $12 .
Explanation:
Let us assume that the price of a adult ticket be x .
Let us assume that the price of a student ticket be y .
As given
ashley school is selling tickets to the annual dance competition.
On the first day of ticket sales the school sold 5 adult tickets and 9 student tickets for a total of $123.
The equation becomes
5x + 9y = 123
As given
The school took in $183 on the second day by selling 13 adult tickets and 12 student tickets.
The equation becomes
13x + 12y = 183
Two equations are
5x + 9y = 123
13x + 12y = 183
Multiply 5x + 9y = 123 by 13 .
65x + 117y = 1599
Mutiply 13x + 12y = 183 by 5
65x + 60y = 915
Subtracted 65x + 60y = 915 from 65x + 117y = 1599 .
65x - 65x + 117y - 60y = 1599 - 915
57y = 684
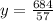
y = $12
Putting y = 12 in the equation
65x + 60 × 12 = 915
65x + 720 = 915
65x = 915 - 720
65x = 195
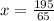
x =$ 3
Therefore the price of an adult ticket is $3 and price of student ticket is $12 .