Hello there!
Question:-
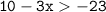
This is a inequality. We need to find the value of x of this inequality.
Solution:-
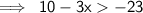
This equation may be rewritten as ,
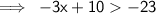
Firstly, Subtract both sides of this equation :-

On Simplification :-
As (+) and (-) equals to (+), So +10-10 will be represented as 10-10.It results to 0.

As (-) and (-) equals to (+), -23-10 will be represented as 23+10. But 23>10. 23 contains a minus (-) sign. The answer is -33.

Divide both sides by -3:-

On Simplification:-
Cancel -3/-3, leave x, then cancel -33/3:-
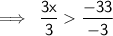
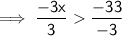
On cancelling -3/-3, 1x is the result, and on cancelling -33/-3, 11 is the result.
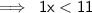
As we know,
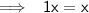
Then , 1x < 11 may be represented as :-
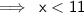
______________________________________
Henceforth, the answer of the inequality is :-
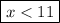
________________________________
I hope this helps!
Please let me know if you have any questions.
~MisterBrian