Question

your school is planning a field trip to the zoo there are two different bus school bus company a has a $35 rental fee plus $5 for each Student Bus Company B has a $95 rental fee plus $3 for each student how many students would need to go in order for the bus to cost the same from both companies

Answer 1

To make the cost the same 30 students would need to go.

Answer 2

With 30 students, both plan would be equal.

Explanation:

We know that Bus A has a $35 rental fee plus $5 for each student, this can be expressed as

`\$35+\$5x`

Where
`x` represents students

Also, we know that Bus B has a $95 rental fee plus $3 for each student, this can be expressed as

`\$95+\$3x`

To find the number of students to both plans be equal, we have to equal both expression and solve for
`x` as follows

`35+5x=95+3x\\5x-3x=95-35\\2x=60\\x=(60)/(2)\\ x=30`

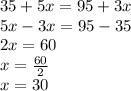
Therefore, with 30 students, both plan would be equal.