Question

A coin is tossed twice. let e e be the event "the first toss shows heads" and f f the event "the second toss shows heads". (a) are the events e e and f f independent? input yes or no here: yes (b) find the probability of showing heads on both toss. input your answer here: preview

Answer 1

huh? couldn’t you retype

Answer 2

a.Yes, Event E and F are independent.

b.
`(1)/(4)`

Explanation:

We are given that a coin is tossed twice.

S={HH,HT,TH,TT}

E={HH,HT}

F={HH,TH}

a.We have to find that event A and event B are independent or not.

We know that when two events A and B are independent then

`P(A)\cdot P(B)=P(A\cap B)`

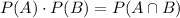
Probability,P(E)=
`(number\;of\;favorable\;cases)/(total\;number\;of cases)`

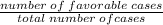
Total number of cases=4

P(E)=
`(2)/(4)=(1)/(2)`

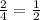
P(F)=
`(2)/(4)=(1)/(2)`

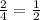
`E\cap F`={HH}

`P(E\cap F)=(1)/(4)`

`P(E)\cdot P(F)=(1)/(2)\cdot (1)/(2)=(1)/(4)`

`\P(E)\cdot P(F)=P(E\cap F)`

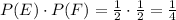
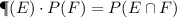
Therefore, Event E and event B are independent.

b.We have to find the probability of showing heads on both toss.

Number of favorable cases={HH}=1

Total number of cases=4

By using the formula of probability

The probability of getting heads on both toss=
`(1)/(4)`