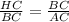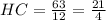Question

In triangle △ABC, ∠ABC=90°, BH is an altitude. Find the missing lengths. AB=9, and AC=12, find HC.

Answer 1

Explanation:

It is given that in △ABC, ∠ABC=90°, BH is an altitude and AB=9 and AC=12, thus using the Pythagoras theorem in △ABC, we get

`(AC)^(2)=(AB)^(2)+(BC)^(2)`

`(12)^(2)=(9)^2+(BC)^2`

`144=81+(BC)^2`

`(BC)^2=63`

`BC=√(63)`

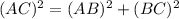
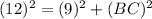
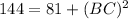
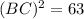
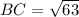
Now, From ΔABC and ΔHBC, we have

∠ABC=∠BHC(each90)

∠ACB=∠HCB (Common)

By AA similarity, ΔABC is similar to ΔHBC.

Thus, using the similarity condition, we get

`(HC)/(BC)=(BC)/(AC)`

`(HC)/(√(63))=(√(63))/(12)`

`HC=(63)/(12)=(21)/(4)`