Make use of prime factorizations:
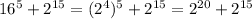
Both terms have a common factor of
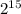 :
:
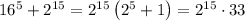
- - -
The second one is not true! We can write
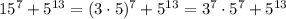
Both terms have a common factor of
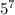 :
:
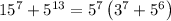
Since
 , and
, and
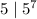 , we'd still have to show that
, we'd still have to show that
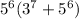 is a multiple of 6. This is impossible, because
is a multiple of 6. This is impossible, because
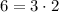 and there is no multiple of 2 that can be factored out.
and there is no multiple of 2 that can be factored out.