Question

Find the missing part.

Answer 1

Answers are :

x = 7.5 , y =
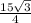`(15√(3) )/(4)` , z =
`(15√(3) )/(2)`

a = 9.375 and b = 5.625

Explanation:

From the attached figure , consider right triangle ABC.

∠B = 60° , BC = 15 {∵ BC = a + b}

We need to find AC = z

Using sin function,

i.e sin(60°) =
`(AC)/(BC)`

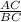
or sin(60°) =
`(AC)/(15)`

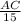
or AC = 15×sin(60°)

or AC =
`(15√(3) )/(2)`

Also, AB = x = 15×cos(60°) =
`(15)/(2) = 7.5`

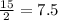
Next,

Consider right triangle ADC

AD = y, AC = z =
`(15√(3) )/(2)`

∠C = 30°

Using sin function to get y.

i.e sin(30°) =
`(AD)/(AC) = (y)/(z)`

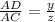
or sin(30°) = \frac{y}{
`(15√(3) )/(2)`}[/tex]

or y =
`(15√(3) )/(2)`×sin(30°)

or y =
`(15√(3) )/(4)`

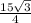
Also, DC = b =
`(15√(3) )/(2)`×cos(30°)

b =
`(45)/(8) = 5.625`

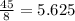
Therefore, a= 15 - b = 15 - 5.625 = 9.375

Hence we got,

x = 7.5 , y =
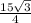`(15√(3) )/(4)` , z =
`(15√(3) )/(2)`

a = 9.375 and b = 5.625

Answer 2

`z = 15[(√(3))/(2)]`

Explanation:

To find the Z-side, we must take the cosine of the 30-degree angle of the main triangle

We know that the cosine of an angle is defined as:

`cos(30) = (adjacent\ side)/(hypotenuse)`

`cos(30) = (√(3))/(2)`

`(√(3))/(2)} = (z)/(15)`

Then:

`z = 15[(√(3))/(2)}]`

Finalmente the side z is:

`z = 15[(√(3))/(2)}]`