Answer:
Answers are :
x = 7.5 , y =
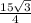 , z =
, z =
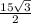
a = 9.375 and b = 5.625
Explanation:
From the attached figure , consider right triangle ABC.
∠B = 60° , BC = 15 {∵ BC = a + b}
We need to find AC = z
Using sin function,
i.e sin(60°) =
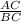
or sin(60°) =
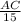
or AC = 15×sin(60°)
or AC =
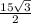
Also, AB = x = 15×cos(60°) =
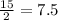
Next,
Consider right triangle ADC
AD = y, AC = z =
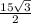
∠C = 30°
Using sin function to get y.
i.e sin(30°) =
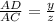
or sin(30°) = \frac{y}{
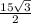 }[/tex]
}[/tex]
or y =
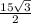 ×sin(30°)
×sin(30°)
or y =
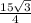
Also, DC = b =
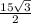 ×cos(30°)
×cos(30°)
b =
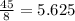
Therefore, a= 15 - b = 15 - 5.625 = 9.375
Hence we got,
x = 7.5 , y =
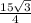 , z =
, z =
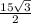
a = 9.375 and b = 5.625