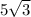Question

\sqrt{27} - \sqrt{ 12} + \sqrt{48 }

Answer 1

`5√(3)`

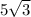
Explanation:

I'm assuming you're asking for most simplified form?

Original Equation:

`√(27) - √(12) + √(48)`

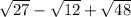
Rewrite sqrt(27) using the exponent property:
`\sqrt[n]{a} * \sqrt[n]{b} = \sqrt[n]{ab}`

`√(9) * √(3) -√(12) + √(48)`

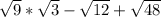
Simplify sqrt(9)

`3√(3) -√(12) + √(48)`

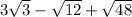
Rewrite the radical sqrt(12)

`3√(3) -√(4)√(3) + √(48)`

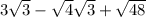
Simplify sqrt(2)

`3 √(3) -2√(3) + √(48)`

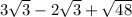
Rewrite the radical sqrt(48)

`3√(3) -2√(3) + √(16)√(3)`

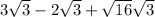
Simplify the sqrt(16)

`3√(3) -2√(3) + 4√(3)`

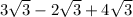
You can think of sqrt(3) as x, in which case you have 3x - 2x + 4x, so you just add the coefficients and leave the sqrt(3) alone.

Subtract 2 from 3

`1√(3) + 4√(3)`

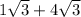
Add 1 and 4

`5√(3)`