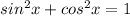Question

What basic trigonometric identity would you use to verify that sin x cos x tan x =1-cos^(2)x?

Answer 1

`\boxed{sin^2x+cos^2x=1}`

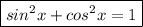
Explanation:

We want to verify that;

`\sin(x) \cos(x) \tan(x)=1-\cos^2(x)`

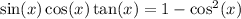
We take only the expression on the left hand side and work to get the expression on the right hand side.

`\sin(x) \cos(x) \tan(x)`

`=\sin(x) \cos(x) (\sin(x))/(\cos(x))`

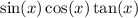
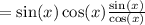
We cancel the common factors to get;

`=\sin(x) * \sin(x)`

`=\sin^2(x)`

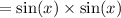
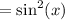
We now use the Pythagorean identity;

`sin^2x+cos^2x=1`

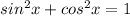
We make
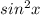`sin^2x` the subject to obtain;

`sin^2x=1-cos^2x`

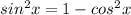
as required.

The basic trigonometric identity we used is
`sin^2x+cos^2x=1`

Answer 2

`tanx=(sinx)/(cosx)\\sin^(2)x=1-cos^(2)x`

Explanation:

1. Keeping on mind that
`tanx=(sinx)/(cosx)`, you have:

`sinx*cosx((sinx)/(cosx))`

2. Simplify it, then you obtain:

`=sinx*sinx\\=sin^(2)x`

3. Keeping on mind that
`sin^(2)x=1-cos^(2)x`, you obtain:

`1-cos^(2)x`