Question

125 tickets were sold for the jazz band concert for a total of $1,022. Students tickets cost $6 each, and general admission tickets cost $10 each. How many of each kind of tickets were sold?

Answer 1

Number of student tickets sold are 57 and general tickets sold are 68.

Explanation:

Let the number of student tickets = x and the number of general tickets = y.

It is given that in total 125 tickets were sold.

So, we have,

`x+y=125`

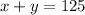
Also, students tickets is sold for $6 each and the general tickets are sold for $10 each.

Since, the total cost of the tickets is $1022.

So, we get,

`6x+10y=1022`

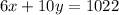
Thus, the system of equations obtained is,

x + y = 125 ........................(1)

6x + 10y = 1022

Multiply equation (1) by 6 gives us,

6x + 6y = 750 ............................(2)

6x + 10y = 1022 .........................(3)

Subtact (2) from (3), we get,

10y - 6y = 1022 - 750

i.e. 4y = 272

i.e. y= 68.

So, equation (1) gives,

x = 125 - y

i.e. y = 125 - 68

i.e. y = 57

Hence, the number of student tickets sold are 57 and general tickets sold are 68.