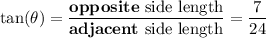Answer:
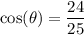
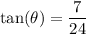
Explanation:
General outline
- Trig ratio Definitions
- Visualizing the triangle for the problem
- Applying the Pythagorean Theorem
- Identifying the other trig ratios
Step 1. Trig ratio definitions
Definitions of primary trig functions
For a given acute angle in a right triangle :
- Sine function:
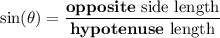
- Cosine function:
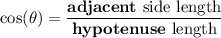
- Tangent function:
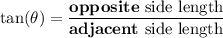
...where the hypotenuse is the side across from the right angle, the opposite side is the side not touching the angle theta, and the adjacent side is the side touching the angle theta (but that isn't the hypotenuse).
We are already given the ratio for the Sine function, so we need to find the Cosine and Tangent function ratios. It will be helpful to visualize what this triangle looks like.
Step 2. Visualizing the triangle for the problem
The given equation states
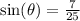 , so there is some right triangle, with a specific angle theta, that has a ratio of sides (opposite to hypotenuse) of 7 to 25. For ease, we'll consider the triangle that has actual side lengths of 7 and 25 for those sides. (See attached diagram)
, so there is some right triangle, with a specific angle theta, that has a ratio of sides (opposite to hypotenuse) of 7 to 25. For ease, we'll consider the triangle that has actual side lengths of 7 and 25 for those sides. (See attached diagram)
Given that information, we can identify that the unknown side length is the adjacent side length. Since the triangle is a right triangle, this value can be found through the Pythagorean Theorem.
Step 3. The Pythagorean Theorem
The Pythagorean Theorem states that for any right triangle,
 where "c" is the length of the hypotenuse of the triangle, and "a" and "b" are the lengths of the other two sides of the triangle (often called "legs"). It does not matter which leg is chosen to be side "a" or side "b" due to the commutative property of addition, but "c" must be the hypotenuse.
where "c" is the length of the hypotenuse of the triangle, and "a" and "b" are the lengths of the other two sides of the triangle (often called "legs"). It does not matter which leg is chosen to be side "a" or side "b" due to the commutative property of addition, but "c" must be the hypotenuse.

Substituting known values, and simplifying...
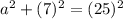

Subtracting 49 from both sides to begin to isolate "a", and simplifying...
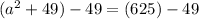
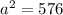
Applying the square root property to isolate "a", and simplifying/calculating...
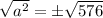
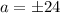
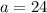 or
or
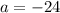
Under the assumption that the triangle is an acute triangle, the adjacent side length is a positive value, so we reject the negative solution, deducing that the adjacent side length must be 24.
Side note: If there is more information in the context of the question that suggests that theta may be larger than 90°, then other factors will need to be taken into account.
Step 4. Identifying the other trig ratios
Returning to the trig ratio definitions, we can identify the requested cosine and tangent ratios