Question

A daylily farm sells a portion of their daylilies and allows a portion to grow and divide. The recursive formula an=1.5(an-1)-100 represents the number of daylilies, a, after n years. After the fifth year, the farmers estimate they have 2225 daylilies. How many daylilies were on the farm after the first year?

Answer 1

c. 600

Explanation:

Answer 2

600 daylilies were on the farm after the first year.

Explanation:

Given : A daylily farm sells a portion of their daylilies and allows a portion to grow and divide. The recursive formula
`a_n=1.5(a_(n-1))-100` represents the number of daylilies, a, after n years. After the fifth year, the farmers estimate they have 2225 daylilies.

To find : How many daylilies were on the farm after the first year?

Solution :

The recursive formula is
`a_n=1.5(a_(n-1))-100`

We have given after the fifth years number of daylilies,
`a_5=2225`

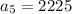
Put n=5 in the formula we get,

`a_5=1.5(a_(5-1))-100`

`2225=1.5(a_(4))-100`

`2325=1.5(a_(4))`

`(2325)/(1.5)=a_4`

`a_4=1550`

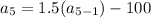
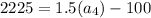
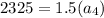
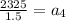
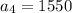
Now, put n=4 in the formula,

`a_4=1.5(a_(4-1))-100`

`1550=1.5(a_(3))-100`

`1650=1.5(a_(3))`

`(1650)/(1.5)=a_3`

`a_3=1100`

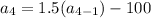
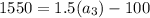
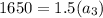
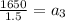
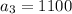
Now, put n=3 in the formula,

`a_3=1.5(a_(3-1))-100`

`1100=1.5(a_(2))-100`

`1200=1.5(a_(2))`

`(1200)/(1.5)=a_2`

`a_2=800`

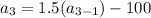
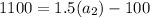
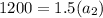
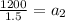
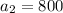
Now, put n=2 in the formula,

`a_2=1.5(a_(2-1))-100`

`800=1.5(a_(1))-100`

`900=1.5(a_(1))`

`(900)/(1.5)=a_1`

`a_1=600`

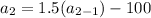
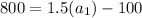
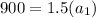
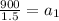
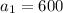
Which means after first year is
`a_1=600`

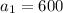
Therefore, 600 daylilies were on the farm after the first year.