Question

∠AED is formed inside a circle by two intersecting chords. If minor arc BD = 70 and minor arc AC = 180, what is the measure of ∠ AED? A) 45° B) 50° C) 55° D) 60°

Answer 1

Answer: The measure of the angle AED is 55°.

Explanation:

Angles of Intersecting Chords Theorem, Two chords intersect in a circle internally ( or inside the circle), then the angle formed is one half the sum of the measure of the arcs intercepted by the angle and its vertical angle.

⇒
`\angle AEC= (180^(\circ)+70^(\circ))/(2)`

`\implies \angle AEC =(250)/(2)=125^(\circ)`

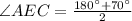
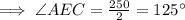
Also, angles AEC and AED are linear pairs,

⇒
`\angle AED+\angle AEC=180^(\circ)`

⇒
`\implies \angle AED = 180^(\circ)-\angle AEC`

`= 180^(/circ)-125^(\circ)=55^(\circ)`

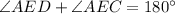
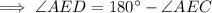
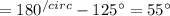
Hence, the measure of the angle AED is 55°.