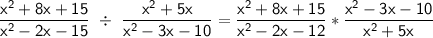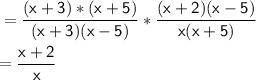Question

Already tried simplifying and dividing, but i didn't get the correct answer. Could a step by step explanation be provided so i know how to do this in the future?

Answer 1

`\sf (x+2)/(x)`

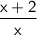
Explanation:

Simplifying the expression:

1. Factorize each expression.

x² + 8x + 15

Sum = 8

Product = 15

Factors = 3 , 5 {When we add 3 & 5 we get 8 and when we multiply 3*5, we get 15}

x² + 8x + 15 = x² + 3x + 5x + 15

= x(x + 3) + 5(x + 3)

= (x + 3)(x + 5)

x² - 2x - 15

Sum = -2

Product = -15

Factors = 3 , (-5) {When we add 3 + (-5) =2 and when we multiply, 3*(-5) = -15}

x² - 2x - 15 = x² + 3x - 5x - 15

=x(x + 3) -5(x + 3)

= (x + 3)(x - 5)

x² + 5x = x( x + 5)

x² - 3x - 10

Sum = -3

Product = -10

Factors = 2 , (-5) {When we add 2 +(-5) = -3 and when we multiply 2 *(-5) = -10}

x² - 3x - 10 = x² + 2x - 5x - 10

=x(x + 2) - 5(x + 2)

= (x + 2)(x - 5)

2. Use KCF method and simplify.

K - keep the first fraction

C - change division to multiplication

F - Flip the second fraction.

`\sf (x^2 + 8x + 15)/(x^2 - 2x - 15) \ / \ (x^2 + 5x)/(x^2 - 3x - 10)=(x^2 + 8x + 15)/(x^2-2x - 12)*(x^2 - 3x - 10)/(x^2 + 5x)`

`\sf = ((x +3)*(x +5))/((x+3)(x - 5))*((x + 2)(x - 5))/(x(x+5)) \\\\= (x + 2)/(x)`