Question

A cable company wants to provide cell phone service for residents on an island. The function for the cost of laying the cable from the island to the mainland is c(x)= 6.500 square root x2+4, where x represents the length of the cable in feet. What are the domain and range of the function?

A) domain: all real numbers
range: all real numbers greater than or equal to 17,000

B) domain: all real numbers greater than or equal to 0
range: all real numbers greater than or equal to 17,000

C) domain: all real numbers greater than or equal to 0
range: all real numbers greater than or equal to 13,000

D) domain: all real numbers greater than or equal to 13,000
range: all real numbers greater than or equal to 0

Answer 1

C.................................................

Explanation:

E2020

Answer 2

C) domain: all real numbers greater than or equal to 0

range: all real numbers greater than or equal to 13,000

Explanation:

We have, the function for the cost of laying cable is given by,

`c(x)= 6500√(x^2+4)`, where x is the length of the cable (in feet).

As, 'x' represents the length of the cable.

We have that, the value of x cannot be negative.

So, x ≥ 0.

Since, the domain of
`c(x)= 6500√(x^2+4)` is the set of points where
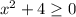`x^2+4\geq 0` and we have that x ≥ 0.

Thus, the domain is 'Set of all real numbers greater than or equal to 0'.

Now, we substitute x= 0 in
`c(x)= 6500√(x^2+4)`.

i.e.
`c(0)= 6500√(0^2+4)`

i.e.
`c(0)= 6500√(4)`

i.e.
`c(0)= 6500* 2`

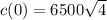
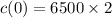
i.e. c(0) = 13000.

So, we get that the vertex point of the function is (0,13000).

Thus, the range is 'All real numbers greater than or equal to 13,000'.