Answer:
A. Yes, they are inverse of each other.
B. Domain and range of the compositions is
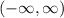 .
.
Explanation:
A. We have,
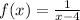 and
and
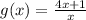 .
.
Now, 'when two functions f and g are inverses of each other, they satisfy the property
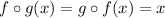 '.
'.
So, we have,
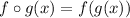
i.e.
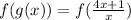
i.e.
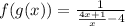
i.e.
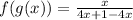
i.e.
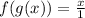
i.e.
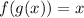
Also,
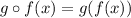
i.e.
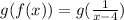
i.e.
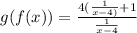
i.e.
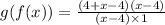
i.e.
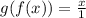
i.e.
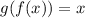
Thus, we get for the given function f and g,
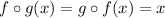 .
.
Hence, they are inverse of each other.
B. Now, as we have,
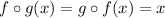 .
.
That is, the composition of the functions is equal to the identity function.
Thus, the domain and range are the set of all real numbers respectively.
So, in the interval notation, we have,
Domain and range of the compositions is
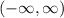 .
.