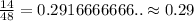Answer: The relative frequencies to the nearest hundredth of the columns of the two-way table is given by :-
A B
Group 1 0.85 0.71
Group 2 0.15 0.29
Explanation:
Given two-way table : A B
Group 1 10 34
Group 2 18 14
Total data value in column A =
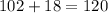
Total data value in column B =
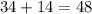
Now, the relative frequency for Group 1 with column A =
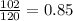
The relative frequency for Group 1 with column B =
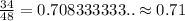
Now, the relative frequency for Group 2 with column A =
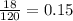
The relative frequency for Group 2 with column B =