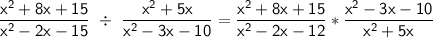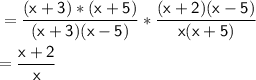Answer:
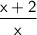
Explanation:
Simplifying the expression:
1. Factorize each expression.
x² + 8x + 15
Sum = 8
Product = 15
Factors = 3 , 5 {When we add 3 & 5 we get 8 and when we multiply 3*5, we get 15}
x² + 8x + 15 = x² + 3x + 5x + 15
= x(x + 3) + 5(x + 3)
= (x + 3)(x + 5)
x² - 2x - 15
Sum = -2
Product = -15
Factors = 3 , (-5) {When we add 3 + (-5) =2 and when we multiply, 3*(-5) = -15}
x² - 2x - 15 = x² + 3x - 5x - 15
=x(x + 3) -5(x + 3)
= (x + 3)(x - 5)
x² + 5x = x( x + 5)
x² - 3x - 10
Sum = -3
Product = -10
Factors = 2 , (-5) {When we add 2 +(-5) = -3 and when we multiply 2 *(-5) = -10}
x² - 3x - 10 = x² + 2x - 5x - 10
=x(x + 2) - 5(x + 2)
= (x + 2)(x - 5)
2. Use KCF method and simplify.
K - keep the first fraction
C - change division to multiplication
F - Flip the second fraction.