Question

Your pendulum clock which advances 1.0 s for every complete oscillation of the pendulum is running perfectly on Earth at a site where the magnitude of the acceleration due to gravity is 9.80 m/s2. You send the clock to a location on the Moon where the magnitude of the acceleration due to gravity is 1.65 m/s2.

Answer 1

As we know that time period of simple pendulum will be

`T = 2\pi \sqrt{(L)/(g)}`

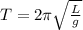
now we will have

time period of a clock on the surface of earth will be 1 s where we have acceleration due to gravity is g = 9.8 m/s/s

now if we took the pendulum to the surface of moon where acceleration due to gravity will be 1.65 m/s/s then this time period will change

so we will say by above equation

`(T_(earth))/(T_(moon)) =\sqrt{ (g_(moon))/(g_(earth))}`

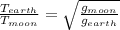
now we will have

`T_(moon) = \sqrt{(g_(earth))/(g_(moon))}T_(earth)`

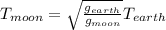
now plug in all data in this

`T_(moon) = \sqrt{(9.8)/(1.65)}(1s)`

`T_(moon) = 2.44 s`

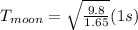
so time period on moon will be 2.44 s