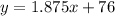Question

PLEASEEEEEEEE HELP

Find the equation of the trend line (line of best fit). Show your work

I'm using the points (34,76) (42,91)

Answer 1

The equation of the trend line is
`y=1.875x+12.25`.

Explanation:

Given : The points (34,76) (42,91).

To find : The equation of the trend line (line of best fit) ?

Solution :

Using two point slope form to find the equation of line.

`(y-y_1)=((y_2-y_1)/(x_2-x_1))(x-x_1)`

Here,
`(x_1,y_1)=(34,76)` and
`(x_2,y_2)=(42,91)`

Substitute the value,

`(y-76)=((91-76)/(42-34))(x-34)`

`(y-76)=((15)/(8))(x-34)`

`(y-76)=(15)/(8)x-(15)/(8)* 34`

`(y-76)=1.875x-63.75`

`y=1.875x-63.75+76`

`y=1.875x+12.25`

Therefore, the equation of the trend line is
`y=1.875x+12.25`.

Answer 2

Using the point-slope form:

The equation of the line is given by:

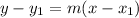`y-y_1 =m(x-x_1)` .....[1] where

m is the slope of the line and
`(x_1, y_1)` is the point on the line.

As per the statement:

Given: Two points i,e (34, 76) and (42, 91)

First calculate slope(m):

Slope is given by:

`\text{Slope} = (y_2-y_1)/(x_2-x_1)`

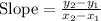
Substitute the given values we have;

`\text{Slope (m)} = (91-76)/(42-34)=(15)/(8)=1.875`

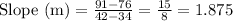
Now, substitute the value of m and (34, 76) in [1] we have;

`y-76 =1.875(x-34)`

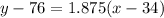
Using distributive property:
`a \cdot (b+c) = a\cdot b+ a\cdot c`

`y-76 =1.875x-63.75`

Add 76 to both sides we get;

`y=1.875x+76`

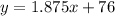
Therefore, the equation of the trend line is:
`y=1.875x+76`