Question

Jackie purchased 3 bottles of water and 2 cups of coffee for the family for $7.35. Ryan bought 4 bottles of water and 1 cup of coffee for his family for 7.15. How much does each bottle of water cost? How much does each cup of coffee cost?

Answer 1

Water = $1.39 Each

Coffee = $1.59 Each

Explanation:

Lets assume that:

W = Water

C = Coffee

Now we have to take the amount of what both Jackie and Ryan Bought.

Jackie got:

`3W + 2C = $7.35`

Ryan got:

`4W + 1C = $7.15`

Now that we have both of their orders, we then can use any of the two equations and find the value of both the water and coffee one at a time.

Let's take Ryans equation and solve for C.

`4W + 1C = $7.15` (NOTE: Let's remove the symbols first to make it clearer)

`4W + 1C = 7.15`

We then transpose the 4W to the other side to solve for C.

`1C = 7.15 - 4W`

`C = 7.15 - 4W`

Now that have a value temporary value for C, we can then substitute it in Jackie's equation.

`3W + 2C = 7.35`

`3W + 2(7.15 - 4W) = 7.35`

We then use the distribution rule.

`3W + 14.30 - 8W = 7.35`

Now we combine LIKE terms.

`3W - 8W = 7.35 - 14.30`

`-5W = -6.95`

Then we divide both sides by -5.

`(-5W)/(-5) = (-6.95)/(-5)`

We end up with:

`W = 1.39`

Now that we have the value of the water, we can then substitute it to find the value of the Coffee.

`3W + 2C = 7.35`

`2C = 7.35 - 3W`

`2C = 7.35 - 3(1.39)`

`2C = 7.35 - 4.17`

`2C = 3.18`

`(2C)/(2) = (3.18)/(2)`

`C = 1.59`

Answer 2

Cost of each cup of coffee is $1.59.

Cost of each bottle of water is $1.39.

Explanation:

Let C be the cost of each cup of coffee and B be the cost of each bottle of water.

We have been given that Jackie purchased 3 bottles of water and 2 cups of coffee for the family. So the cost of 3 bottles of water will be 3B and cost of 2 cups of coffee will be 2C.

As Jackie spent $7.35 on these items, so we can represent this information in an equation as:

`3B+2C=7.35...(1)`

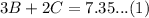
We are also told that Ryan bought 4 bottles of water and 1 cup of coffee for his family. So the cost of 4 bottles of water will be 4B and cost of 1 cup of coffee will be C.

As Ryan spent $7.15 on these items, so we can represent this information in an equation as:

`4B+C=7.15...(2)`

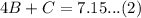
To find the cost of one cup of coffee we will solve our system of equations using substitution method.

From equation (2) we will get,

`C=7.15-4B`

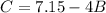
Substituting this value in equation (1) we will get,

`3B+2(7.15-4B)=7.35`

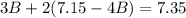
Upon using distributive property we will get,

`3B+14.30-8B=7.35`

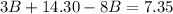
Let us combine like terms.

`3B-8B+14.30-14.30=7.35-14.30`

`-5B=-6.95`

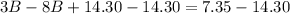
Upon multiplying both sides of our equation by -5 we will get,

`(-5B)/(-5)=(-6.95)/(-5)`

`B=1.39`

Therefore, the cost of one bottle of water is $1.39.

Upon substituting B=1.39 in equation (2) we will get,

`4*1.39+C=7.15`

`5.56+C=7.15`

Upon subtracting 5.56 from both sides of our equation we will get,

`5.56-5.56+C=7.15-5.56`

`C=1.59`

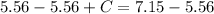
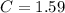
Therefore, the cost of each coffee is $1.59.