Question

a carnival sold tickets for $1.50 for adults and $1.00 for students. there were 54 tickets sold for a total of $70.50. write a system of equations to represent the number of adult tickets,x, and the number of student tickets,y. find the solution and explain what it means. I'll help you if you help me

Answer 1

Answer:

The number of adult tickets are 33 and the number of student tickets are 21 .

Explanation:

As

The number of adult tickets x and the number of student tickets y.

As given

A carnival sold tickets for $1.50 for adults and $1.00 for students.

There were 54 tickets sold for a total of $70.50.

Equations becomes

x + y = 54

1.50x + 1.00y = 54 × 70.50

Simplify the above

`(150x)/(100) + (100y)/(100) = (7050)/(100)`

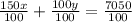
150x + 100y =7050

Two equations are

x + y = 54

150x + 100y =7050

Multiply x + y = 54 by 150 from 150x + 100y =7050

150x - 150x + 100y - 150y = 7050 - 8100

-50y = -1050

50y = 1050

`y = (1050)/(50)`

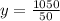
y = 21

Putting the value of y in the equation .

x + 21 = 54

x = 54 - 21

x = 33

Therefore the number of adult tickets are 33 and the number of student tickets are 21 .