Answer:
29.04 feet
Explanation:
Given : A sailor is looking at a kite. If he is looking at the kite at an angle of elevation of 36
The distance from the boat to the point where the kite is directly overhead is 40 feet
To Find: how high is the kite
Solution :
Refer the attached figure
Since we are given that The distance from the boat to the point where the kite is directly overhead is 40 feet i.e. AB = 40 feet
Since we are also given that angle of elevation = 36° i.e. ∠BAC =36°
So we need to find how high is the kite i.e. BC
So, we will use trigonometric ratio
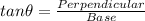
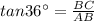
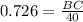
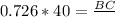
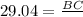
Thus the length of BC = 29.04 feet
Hence the kite is 29.04 feet high