Question

Parks is wearing several rubber bracelets one third of the bracelets are tie-dye 1/6 are blue and 1/3 of the remainder are camouflage if Parks wears 2 camouflage bracelets how many bracelets does he have on

Answer 1

Answer: There are 12 bracelets he have on in total.

Explanation:

Since we have given that

Number of bracelets are tie-dye is given by

`(1)/(3)`

Number of bracelets that are blue is given by

`(1)/(6)`

Total number of bracelets used till now is given by

`(1)/(3)+(1)/(6)\\\\=(2+1)/(6)\\\\=(3)/(6)\\\\ =(1)/(2)`

Remaining bracelets are given by

`1-(1)/(2)\\\\=(1)/(2)`

Number of bracelets that are camouflage is given by

`(1)/(3)* (1)/(2)=(1)/(6)`

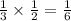
Let the total number of bracelets he have on be 'x'.

Number of camouflage bracelets he wears = 2

According to question, we have

`(1)/(6)* x=2\\\\x=6* 2=12`

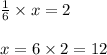
Hence, there are 12 bracelets he have on in total.