Question

The length of triangle base is 26. A line, which is parallel to the base divides the triangle into two equal area parts. Find the length of the segment between triangle legs.

Answer 1

Explanation:

It is given that the length of triangle base is 26, then let ABC be the triangle and BC be the base of the triangle=26.Let DE be the parallel line to the base that divides triangle ABC into two equal area parts.

Now, Let AD=a, DB=b, DE=c, AE=d and EC=e, then

Since, triangle ABC is similar to triangle ADE, thus using basic proportions, we get

`(AD)/(AB)=(DE)/(BC)=(AE)/(AC)`

`(AD)/(AD+DB)=(DE)/(BC)=(AE)/(AE+EC)`

`(a)/(a+b)=(c)/(26)=(d)/(d+e)`

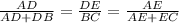
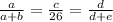
Taking the first two equalities,we get

`(a)/(a+b)=(c)/(26)`

`c=(26a)/(a+b)`

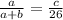
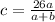
Thus, the length of the segment between triangle legs is
`(26a)/(a+b)`