Question

The base of a triangle exceeds the height by 7 centimeters. If the area is 400 square centimeters, find the length of the base and the height of the triangle.

Answer 1

Base = 32 cm

Height = 25 cm

Explanation:

Area of a triangle can be calculated as:

`Area = (1)/(2)* Base * Height`

We are given that the base of triangle exceeds the height by 7 cm. This can be expressed in an equation form as:

Base = Height + 7

Lets use B to represent base and H to represent height

B = H + 7

The equation of area can be stated as:

`Area=(1)/(2)bh\\\\ Area=(1)/(2)(h+7)(h)\\\\ 400=(1)/(2)h(h+7)\\\\ 800=h^(2)+7h\\\\ h^(2)+7h-800=0`

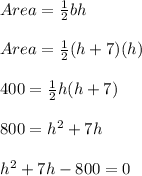
This is a quadratic equation which can be solved using a quadratic equation as shown below:

`h=(-7+-√(49-4(1)(-800)) )/(2(1)) \\\\ h=(-7+-57)/(2)\\\\h=-32,25`

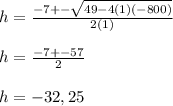
Since the height cannot be negative, we'll consider the positive value only i.e height is equal to 25 cm.

Therefore, the length of base will be 25 + 7 = 32 cm.