Answer: 20 meters.
Explanation:
1. Keeping on mind the information shown in the figure attached and the similarity of both triangles, you can calculate the height of the tree (h) as you can see below:
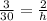
2. Now, you must solve for the height. So, you obtain the following result:

3. Therefore, the height of the tree is 20 meters.