Question

A cone with volume 1350 m³ is dilated by a scale factor of 1/3.

What is the volume of the resulting cone?



Enter your answer in the box.


______ m³

Answer 1

50 m

Explanation:

just took the test to prove it was the right answer:)

Answer 2

Answer: The answer is 50 m³.

Step-by-step explanation: We are given to find the volume of the cone cone after being dilated by a factor of one-third from a cone with volume 1350 m³.

The volume of a cone with base radius 'r' units and height 'h' units is given by

`V=(1)/(3)\pi r^2h.`

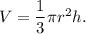
Therefore, if 'r' is the radius of the base of original cone and 'h' is the height, then we can write

`V=(1)/(3)\pi r^2h=1350\\\\\\\Rightarrow \pi r^2h=4050.`

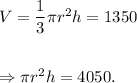
Now, if we dilate the cone by a scale factor of
`(1)/(3)`, then the radius and height will become one-third of the original one.

Therefore, the volume of the dilated cone will be

`V_d=(1)/(3)\pi ((r)/(3))^2(h)/(3)=(1)/(81)* \pi r^2h=(1)/(81)* 4050=50.`

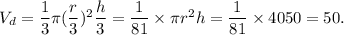
Thus, the volume of the resulting cone will be 50 m³.