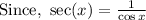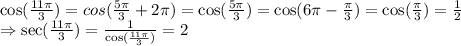Question

Find the exact value of each of the following. In each case, show your work and explain the steps you take to find the value.

(a) sin 17π/6
(b) tan 13π/4
(c) sec 11π/3

Answer 1

Answer: a)
`(1)/(2)`

b) 1

c) 2

Explanation:

(a) sin 17π/6

It is known that the value of sin x repeat after an interval of
`2\pi\ or\ 360^(\circ)`

∴
`\sin(17\pi)/(6)=\sin2(5\pi)/(6)=\sin(2\pi+(5)/(6)\pi)=\sin{(5)/(6)\pi}=\sin(\pi-(\pi)/(6))=\sin((\pi)/(6))=(1)/(2)`

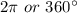
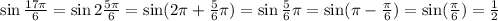
[Since the value of sin x is positive in 2nd quadrant]

(b) tan 13π/4

It is known that the value of sin x repeat after an interval of
`\pi\ or\ 180^(\circ)`

∴
`\tan(13\pi)/(4)=\tan(3\pi+(\pi)/(4))=\tan{(\pi)/(4)}=1`

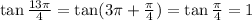
(c) sec 11π/3

`\text{Since, }\sec(x)=(1)/(\cos x)`

`\cos((11\pi)/(3))=cos((5\pi)/(3)+2\pi)=\cos((5\pi)/(3))=\cos(6\pi-(\pi)/(3))=\cos((\pi)/(3))=(1)/(2)\\\Rightarrow\sec((11\pi)/(3))=(1)/(\cos((11\pi)/(3)))=2`