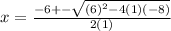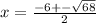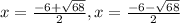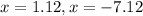Question

Use the quadratic formula to solve the equation. If necessary, round to the nearest hundredth.

x^2 - 8 = -6x

a. –7.12, 1.12
b. 7.12, –1.12
c. 7.12, 1.12
d. –7.12, –1.12

Answer 1

The correct answer option is a. –7.12, 1.12.

Explanation:

We are given the following equation and we are to solve it using the quadratic formula:

`x^2 - 8 = -6x`

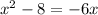
Re-arranging this equation in order of decreasing power:

`x^(2) + 6x - 8 = 0`

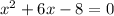
Using the quadratic formula:

`x = \frac {-b + - √(b^2 - 4ac) }{2a}`

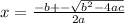
Substituting the given values in the formula to get:

`x=(-6+-√((6)^2-4(1)(-8)) )/(2(1))`

`x=(-6+-√(68) )/(2)`

`x=(-6+√(68) )/(2) , x= (-6-√(68) )/(2)`

`x=1.12, x=-7.12`

Answer 2

x = -7.12, 1.12

Explanation:

We are given an equation and asked to solve it with quadratic formula

Quadratic formula is given as:

`x = \frac{-b +- \sqrt{b^(2)-4ac } }{2a}`

Given equation: x² - 8 = -6x

Rewriting the equation

x² - 8 + 6x = 0

x² + 6x - 8 = 0

Where a = 1; b = 6; c = -8

Putting the values of a, b and c in quadratic formula

`x = \frac{-6 +- \sqrt{6^(2)-4(1)(-8) } }{2(1)}`

`x = (-6 +- √(36+32))/(2)`

`x = (-6 +- √(68))/(2)`

`x = (-6 +- 8.25)/(2)`

`x = (-6 + 8.25)/(2)`

x = 1.12

`x = (-6 - 8.25)/(2)`

x = -7.12

x = -7.12, 1.12