Question

What are the solutions of the equation?

16x^2 + 24x + 5 = 5

a. 1/4, 5/4
b. -1/4, -5/4
c. -1/4, 5/4
d. 1/4 , -5/4

Answer 1

B

Explanation:

you have the wrong equation posted.

if you meant to post
`16x^2+24x+5=0`

the answer would be B.

Answer 2

For this case, we have the following quadratic equation:

`16x ^ 2 + 24x + 5 = 5\\16x ^ 2 + 24x + 5-5 = 0\\16x ^ 2 + 24x = 0`

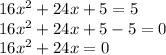
If we divide between 4 on both sides to simplify we have:

`4x ^ 2 + 6x = 0`

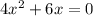
This equation is of the form:

`ax ^ 2 + bx + c = 0`

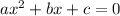
Where:

`a = 4\\b = 6\\c = 0`

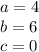
Its roots are given by:

`x = \frac {-b \pm \sqrt {b ^ 2-4 (a) (c)}} {2 (a)}\\x = \frac {-6 \pm \sqrt {6 ^ 2-4 (4) (0)}} {2 (4)}\\x = \frac {-6 \pm \sqrt {36}} {8}\\x = \frac {-6 \pm6} {8}`

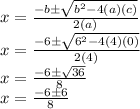
So, we have two roots:

`x_ {1} = \frac {-6 + 6} {8} = 0\\x_ {2} = \frac {-6-6} {8} = - \frac {12} {8} = - \frac {3} {2}`

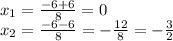
Answer:

The roots are:
`x_ {1} = 0\ and\ x_ {2} = - \frac {3} {2}`

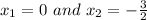
None of the options given are solution