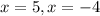Answer:
The correct answer option is d. 5, -4.
Explanation:
We are given the following equation and we are to solve it using the quadratic formula:
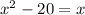
Re-arranging this equation in order of decreasing power:
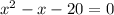
Using the quadratic formula:
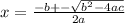
Substituting the given values in the formula to get:

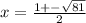
![x=(1+√(81) )/(2) , x= \frac{1-√(81){2}]()