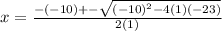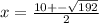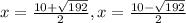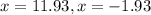Question

Use the quadratic formula to solve the equation. If necessary, round to the nearest hundredth.

x^2 - 23 = 10x

a. -1.93, 11.93
b. 1.93, -11.93
c. 1.93, 11.93
d. -1.93, -11.93

Answer 1

The correct answer option is a. -1.93, 11.93.

Explanation:

We are given the following equation and we are to solve it using the quadratic formula:

`x^2 - 23 = 10x`

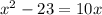
Re-arranging this equation in order of decreasing power:

`x^(2) - 10x - 23 = 0`

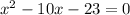
Using the quadratic formula:

`x = \frac {-b + - √(b^2 - 4ac) }{2a}`

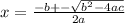
Substituting the given values in the formula to get:

`x=(-(-10)+-√((-10)^2-4(1)(-23)) )/(2(1))`

`x=(10+-√(192) )/(2)`

`x=(10+√(192) )/(2) , x=(10-√(192) )/(2)`

`x=11.93, x=-1.93`

Answer 2

Option B. 1.93, -11.93 is the right answer.

Explanation:

Here the given equation is x²-23 = 10x and we have to solve the equation for the value of x.

First we simplify the equation to bring in the shape of ax²+bx+c=0

x²-23 = 10x

(x²-23)-10x = 10x-10x

x²-10x -23 = 0

Now we the formula for the value of
`x= \frac{-b\pm \sqrt{b^(2)-4ac}}{2a}`

`x=\frac{10\pm \sqrt{(-10)^(2)-4(1)(-23)}}{2(1)}`

`x=(-10\pm  √(100+92))/(2)`

`x= (-10\pm √(192))/(2)`

`x=(-10\pm 4√(12))/(2)`

`x=-5\pm 2√(12)`
`= -5\pm (2* 3.464)`
`= -5\pm 6.93`

Now x = (-5+6.93) = 1.93

and x = (-5-6.93) = -11.93