Question

The diagonals of a quadrilaretral intersect at (-1,4). One of the sides of the quadrilateral is bounded by (2,7) and (-3,5)

Determine the coordinates of the other side In order for the quadrilaretral to be a square.

Answer:_________

Answer 1

Properties of Square

1. All sides are equal.

2. Opposite sides are parallel.

3. Diagonals are equal and bisect each other at right angles.

As, given point of intersection of diagonals of square is (-1,4).

And, One of the sides of the quadrilateral is bounded by (2,7) and (-3,5).

Drawn the picture of square below,

Let, the third and fourth vertices of square be (x,y) and (p,q).

As, diagonals of square bisect each other. So,

`(x+2)/(2)=-1\\\\ x +2=-2\\\\ x=-2-2\\\\ x=-4\\\\ (y+7)/(2)=4\\\\ y+7=8\\\\ y=8-7\\\\ y=1\\\\ (p-3)/(2)=-1\\\\ p-3=-2\\\\ p=3-2\\\\ p=1 \\\\ (q+5)/(2)=4\\\\ q+5=8\\\\ q=8-5\\\\ q=3`

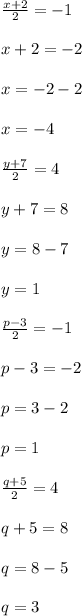
So, third and fourth vertices are (-4,1) and (1,3).