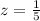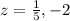Question

What are the solutions of the equation?

5z^2 + 9z - 2 = 0

a. 1, -2
b. 1, 2
c. 1/5, -2
d. 1/5, 2

Answer 1

c. 1/5, -2

Explanation:

We are given the following equation and we are to solve it by factorizing it:

`5z^2 + 9z - 2 = 0`

We are to find factors of -10 such that when multiplied they give a product of -10 and when added they give a result of 9.

`5z^2 - z + 10z - 2 = 0`

`z (5z-1) + 2(5z-1) = 0`

`(z+2)(5z-1)=0`

`z=-2, z= (1)/(5)`

Therefore, the correct answer option is c. 1/5, -2.

Answer 2

`(1)/(5),-2`

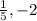
Explanation:

We are given an equation 5z² + 9z - 2 = 0 and we are to find possible values of z by solving that equation

We will do the task by factorization method:

5z² + 9z - 2 = 0

We can break the midterm (+9z) in two terms such that when they are multiplied the result is -10z² i.e. equal to product of first and third term of the equation above and their sum is equal to 9z

5z² + 10z - z - 2 = 0

5z(z + 2) - 1(z + 2) = 0

taking z+2 common in the above equation

(z+2)(5z-1) = 0

We can write above equation as

(x+2) = 0 (5z-1) = 0

x = -2; 5z = 1

`z=(1)/(5)`

`z=(1)/(5),-2`