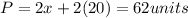Question

The width of a rectangle is 20 units. Can the perimeter P of the rectangle be 64 units when its length x is 11 units?

No, because P = 2x + 2(20)
No, because P ≠ 2x + 2(20)
Yes, because P ≠ 2x + 2(20)
Yes, because P = 2x + 2(20)

Answer 1

Answer: No, because
`P=2x+2(20)`

Explanation:

1. You have that the formula for calculate the perimeter of a rectangle is:

`P=2L+2W`

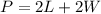
Where L is the lenght and W is the width.

2. You know that the width of a rectangle is 20 units and the lenght x is 11 units. Then, when you substitute values, you obtain:

`P=2x+2W=2(11units)+2(20units)=62units`

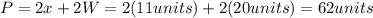
3. Therefore, you can conclude that the perimeter cannot be 64 units, because if the lenght is 11 units and the width is 20 units, the perimeter is 62 units and not 64 units:

`P=2x+2(20)=62units`