Question

GH bisects FGI. Find the measure of HGI

•15°
•21°
•10°
•8°

Answer 1

Option B is correct.

the measure of angle HGI is 21°

Explanation:

By Angle bisector definition:

A line that bisects the angle into equal angle

From the given figure, we have;

`\angle FGH = (2x+1)^(\circ)` and
`\angle HGI = (3x-9)^(\circ)`

it is given that: GH bisects ∠FGI.

then by definition:

`\angle FGH = \angle HGI`

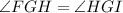
Substitute the given values we have;

`2x+1 = 3x -9`

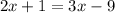
Add 9 to both sides we get;

`2x+10= 3x`

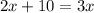
Subtract 2x from both sides we get;

`10= x`

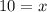
or

`x= 10`

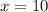
then;

`\angle HGI = 3x-9 = 3(10)-9 = 30-9 = 21^(\circ)`

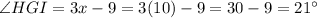
Therefore, the measure of angle HGI is 21°

Answer 2

m<HGI=21°

Explanation:

we know that

If GH bisects m<FGI then

m<FGH=m<HGI

substitute the values

(2x+1)°=(3x-9)°

solve for x

3x-2x=1+9

x=10°

The measure of angle HGI is equal to

(3x-9)° ------> substitute the value of x

3*10-9=21°

m<HGI=21°