Question

molten iron fills a mould, which has a volume of 200 cm cubed. Calculate the volume when the iron cools and solidifies. Molten iron has a density of 7.0g/cm cubed. In its solid state, iron has a density of 8.0g/cm cubed.

Answer 1

901 Shelby drive look alive look alive

Answer 2

As we know that mass of the iron will remain same in solid state as well as in molten state as per mass conservation theory

Now we can say

`m_(initial) = m_(final)`

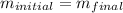
since mass is the product of volume and density so we can say

`V_i \rho_i = V_(final)\rho_(final)`

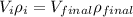
now from above equation we have

`(200 cm^3)(7 g/cm^3) = V_(final)(8 g/cm^3)`

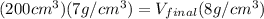
now by solving above equation we have

`V_(final) = (7)/(8) (200 cm^3)`

`V_(final) = 175 cm^3`

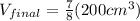
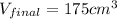
so final volume after it get solidify will become 175 cm^3