Answer:
y < 3x + 2
Explanation:
We will be solving this in slope-intercept form, which is a form that gives us the slope and the y-intercept of the graph explicitly:
 , m is the slope and b is the y-intercept
, m is the slope and b is the y-intercept
We are given that everything to the left of the resulting line is shaded, so we know that the inequality sign will be < (less than). That already eliminates the second and fourth options. We also know the y-intercept, or the point where the graph crosses the y-axis and x is 0. because it is given to us (2, which comes from the point (0,2)). To figure out the slope, we can use the formula since we are given two points [(-3, -7) and (0, 2)] the line passes through. The formula, which is mapped out below, tells us that the slope is just the difference in rise (vertical movement) divided by the difference in run (horizontal movement).
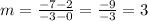
Now we have all the information we need to find the inequality. The slope is 3, the y-intercept is 2, and the sign is <. The first inequality fits these criteria, meaning the correct linear inequality is y < 3x + 2