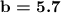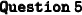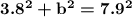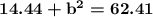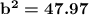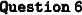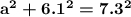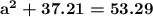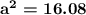
- Side length = 7 cm,
- Side length = 5 cm.
This is how it's done.

There's a special formula that we can use if we need to find the longest side of a right triangle. Fortunately, all of these triangles are right ones! Good.
The formula is.
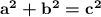 . This formula is known as Pythagoras' Theorem. This formula only works for right triangles.
. This formula is known as Pythagoras' Theorem. This formula only works for right triangles.
Since we have a and b, we can just put in the values (7 for a and 5 for b), And then simplify!
 | 7^2 simplifies to 49, and 5^2 simplifies to 25
| 7^2 simplifies to 49, and 5^2 simplifies to 25
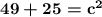 . | add
. | add
 | square root both sides
| square root both sides
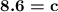 . | the answer is given to 1 decimal place, as the problem required
. | the answer is given to 1 decimal place, as the problem required

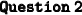
Once more, we're given two sides, and asked to find the third one,
which is still the longest side.
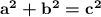 is still the formula used here
is still the formula used here
Put in 5 for a and 3 for b.
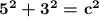 | 5^2 simplifies to 25, and 3^2 simplifies to 9
| 5^2 simplifies to 25, and 3^2 simplifies to 9
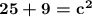 | add
| add
 | square root both sides
| square root both sides
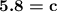 | once again it's given to one decimal place
| once again it's given to one decimal place

This problem is solved the exact same way
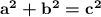
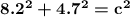
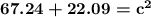

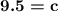 , rounded to one D.P.
, rounded to one D.P.

Here we have the longest side and one side length-:
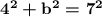 | 4^2 simplifies to 16 and 7^2 simplifies to 49
| 4^2 simplifies to 16 and 7^2 simplifies to 49
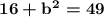 | subtract 16 from both sides
| subtract 16 from both sides
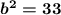 | square root both sides
| square root both sides