Question

True or False: The graph of y=f(bx) is a horizontal compression of the graph y=f(x) if b<1

Answer 1

The given statement is false.

Explanation:

if y = f(x) be a function then the transformation of the type :

y = f(bx) gives a horizontal stretch when 0 < b < 1 and

a horizontal compression when b > 1.

Hence, the given statement that:

The graph of y=f(bx) is a horizontal compression of the graph y=f(x) if b<1 is a false statement.

Also we can consider example of sine function that is we can see the graph of:

`y=\sin x`

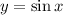
and
`y=\sin {(x)/(2)}`

We could clearly see that the graph of the transformation is a horizontal stretch.