Answer:
g(x)= x+1
Explanation:
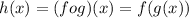
Given
![f(x)= \sqrt[3]{x+2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/d0vq25a0jtrkwcashthtt81bxqu87ff63m.png) ,
,
![f(x)= \sqrt[3]{x+3}](https://img.qammunity.org/2020/formulas/mathematics/high-school/6676rydmbsrt0r5hp72o53epg2j70ftnnm.png)
![f(g(x))= \sqrt[3]{x+3}](https://img.qammunity.org/2020/formulas/mathematics/high-school/p5f7j9fx9r3s5uf0lhl4rk46onf95m6hdr.png)
![f(x)= \sqrt[3]{x+2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/d0vq25a0jtrkwcashthtt81bxqu87ff63m.png)
Replace x with g(x)
![f(g(x))= \sqrt[3]{g(x)+2}](https://img.qammunity.org/2020/formulas/mathematics/high-school/wbl5ng84ep09b31ft7ar7luq9hqfwcqkbk.png)
Now we need to find out what we plug in for g(X) to get x+3 under the radical
g(x) +2 is under the radical. we need x+3 , so we replace g(x) with x+`
So g(x)+2 becomes x+1+2 is x+3
Hence g(x) is x+1