Question

What is the length of the segment, endpoints of which are intersections of parabolas y=x2? 11 4 x? 7 4 and y=? 7 8 x2+x+ 31 8 ?

Answer 1

The length of the line segment is 5 unit.

Explanation:

The given equations are

`y=x^2-(11)/(4)x-(7)/(4)` .... (1)

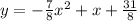`y=-(7)/(8)x^2+x+(31)/(8)` .... (2)

Equate both equations.

`x^2-(11)/(4)x-(7)/(4)=-(7)/(8)x^2+x+(31)/(8)`

`(1)/(4)(4 x^2 - 11 x - 7) = (1)/(8)(-7 x^2 + 8 x + 31)`

`2(4 x^2 - 11 x - 7) = -7 x^2 + 8 x + 31`

`8 x^2 - 22 x - 14 = -7 x^2 + 8 x + 31`

`15 x^2 - 30 x - 45 = 0`

`15 x^2 - 45x+30x - 45 = 0`

`15x(x-3)x+15(x-3)=0`

`15(x+1)(x-3)x=0`

`x=-1,3`

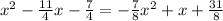
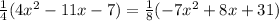
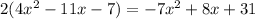
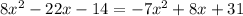
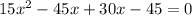
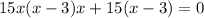
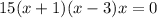
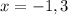
The value of y at x=-1.

`y=(-1)^2-(11)/(4)(-1)-(7)/(4)=2`

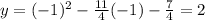
The value of y at x=3.

`y=(3)^2-(11)/(4)(3)-(7)/(4)=-1`

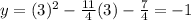
Therefore the intersection points of given parabolas are (-1,2) and (3,-1).

The length of line segment is

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((3-(-1))^2+(-1-2)^2)`

`d=√(16+9)`

`d=5`

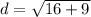
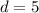
Therefore the length of the line segment is 5 unit.