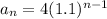Answer:
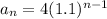
Explanation:
Since, the initial number of hot dogs = 4
According to the question,
The number of hot dogs is increasing by 110% of that of previous day,
Thus, the number of hot dog in first day = 4
Second day = 110 % of 4 = 4.4
Third day = 110% of 4.4 = 4.84
Fourth day = 110% of 4.84 = 5.324
So on.......
Thus, we get a GP,
4, 4.4, 4.84, 5.324 ..........................
That having common ratio, d = 1.1
And, first term, a = 4
Since, the nth term of the GP,

Hence, the required explicit formula of the given situation,