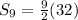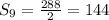Question

An arithmetic series a consists of consecutive integers that are multiples of 4 what is the sum of the first 9 terms of this sequence if the first term is 0

Answer 1

Answer: 144

Explanation:

Since, the first 9 multiple of 4 starts from 0 are,

0, 4, 8, 12, 16, 20, ................

Which is an AP,

Having the first term,
`a_1 = 0`

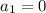
And, the successive difference, d = 4,

Since, the sum of the n term of an AP,

`S_n = (n)/(2)[2a + (n-1)d]`

Hence the sum of 9 term of the above AP,

`S_9 = (9)/(2)[2* 0 + (9-1)* 4]`

`S_9 = (9)/(2)(0 + 8* 4)`

`S_9 = (9)/(2)(32)`

`S_9 = (288)/(2)=144`