Question

2 tangents are drawn from a point a which is 37 cm from the center of the circle. The diameter of the circle is 24 cm. What is the length of each tangent from point a to the point of the tangency?

Answer 1

Answer: 35 cm

Explanation:

Given : Diameter of a circle= 24 cm

Let r be the radius of the circle.

then
`r=(d)/(2)=12\ cm`

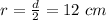
Since a tangent is always at right angles to the radius where it touches the circle.

Join the point A to the center of the circle such that it will become a right triangle with 37 cm as the longest sides [since it is the side opposite to the right angle.]

Let x denote the length of the tangents.

By Pythagoras theorem, we have

`r^2+x^2=(37)^2\\\Rightarrow\ (12)^2+x^2=1369\\\Rightarrow\ x^2=1369-144\\\Rightarrow\ x^2=1225\\\Rightarrow\ x=35`

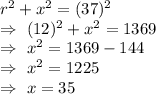
Hence, the length of each tangent from point a to the point of the tangency=35 cm