(a) The inequality follows from the binomial theorem.
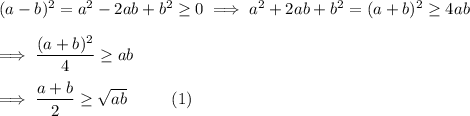
By the same reasoning,
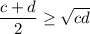
Adding these results together, we have
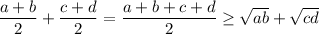
and since
 and
and
 are both positive, they also satisfy the AM-GM inequality,
are both positive, they also satisfy the AM-GM inequality,
![\frac{√(ab) + √(cd)}2 \ge \sqrt{√(ab)*√(cd)} = \sqrt[4]{abcd}](https://img.qammunity.org/2023/formulas/mathematics/college/zchu4wr41c90q83denyxefympenu0k1zgt.png)
and the 4-variable result follows,
![\frac{a+b+c+d}2 \ge 2*\frac{√(ab)+√(cd)}2 \ge 2 \sqrt[4]{abcd} \\\\ \implies \frac{a+b+c+d}4 \ge \sqrt[4]{abcd} ~~~~~~~~ (2)](https://img.qammunity.org/2023/formulas/mathematics/college/fym499el8qkz2l4xrv6nl33oro7i5yo6uc.png)
(b.i) With
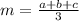 , we have
, we have
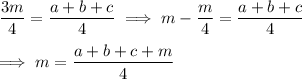
(b.ii) From (2) it follows that
![\frac{a+b+c+m}4 \ge \sqrt[4]{abcm} = \sqrt[4]{abc*\frac{a+b+c+m}4}](https://img.qammunity.org/2023/formulas/mathematics/college/wn7u95lpc5rq55zrmenceax5mj5nhlxc8m.png)
Using the result from (b.i), this is equivalent to
![\frac{a+b+c}3 \ge \sqrt[4]{abc*\frac{a+b+c}3}](https://img.qammunity.org/2023/formulas/mathematics/college/8xsnfwpxzpwj699w3qei9gb4alyes9dneh.png)
Take 4th powers on both sides.
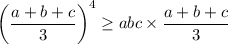
Divide both sides by
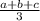 .
.
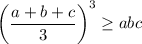
Finally, take the cube root of both sides.
![\frac{a+b+c}3 \ge \sqrt[3]{abc}](https://img.qammunity.org/2023/formulas/mathematics/college/v5qatr69ir9mfmjp8d5l5kyjfsvepyoxsd.png)
as required.