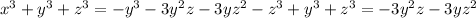If x+y+z=0 what is the value of {x}^(3) + {y}^(3) + {z}^(3)

Question

If x+y+z=0 what is the value of

`{x}^(3) + {y}^(3) + {z}^(3)`

Answer 1

I don't think that there's a unique answer, because it depends on the numbers you choose: for example, if you pick
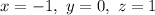`x = -1,\ y=0,\ z= 1`, then you have

`x+y+z=0,\quad x^3+y^3+z^3 = 0`

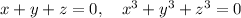
But for example, if you if you pick
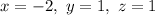`x = -2,\ y=1,\ z= 1`, then you have

`x+y+z=0,\quad x^3+y^3+z^3 = -8+1+1 = -6`

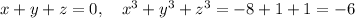
Even if you wanted to use formula, you can at most solve one variable in terms of the other two:

`x+y+z \iff x=-y-z \iff x^3 = -y^3 - 3 y^2 z - 3 y z^2 - z^3`

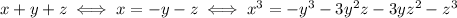
and thus

`x^3+y^3+z^3 = -y^3 - 3 y^2 z - 3 y z^2 - z^3+y^3+z^3 = - 3 y^2 z - 3 y z^2`

Answer 2

`x {}^(3) + y {}^(3) + z {}^(3) = (x + y + z)(x {}^(2) + y {}^(2) + z {}^(2) - xy - yz - xz) + 3xyz`
if we put the value of x+y+z in the equation so the 3xyz will remain so the answer is 3xyz.